Hydrodynamics in Quantum Many-Body Systems
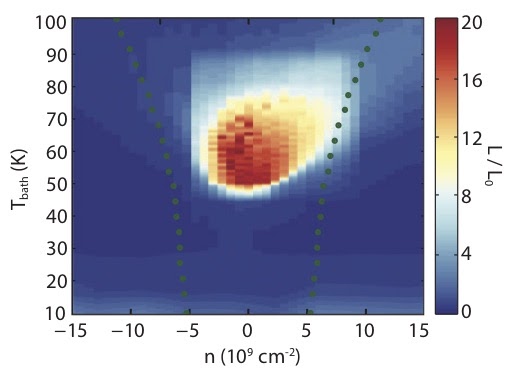
We study the onset and consequences of hydrodynamic behavior in quantum systems with many degrees of freedom. The emergent fluid-like behavior of these systems provides a simple and tractable limit in which to study strongly correlated quantum matter, a problem which is otherwise largely intractable. We are especially interested in the study of hydrodynamic behavior in electronic liquids in experimentally realized solid-state devices, including graphene, where we actively work with experimental groups to probe the hydrodynamic regime, including using state-of-the-art imaging. We have also discovered an infinite new family of hydrodynamic theories describing fracton quantum matter, along with other kinds of constrained quantum systems. More recently, we have discovered higher-dimensional (fractonic) non-equilibrium fixed points arising from the breakdown of hydrodynamics.
Quantum Information Dynamics
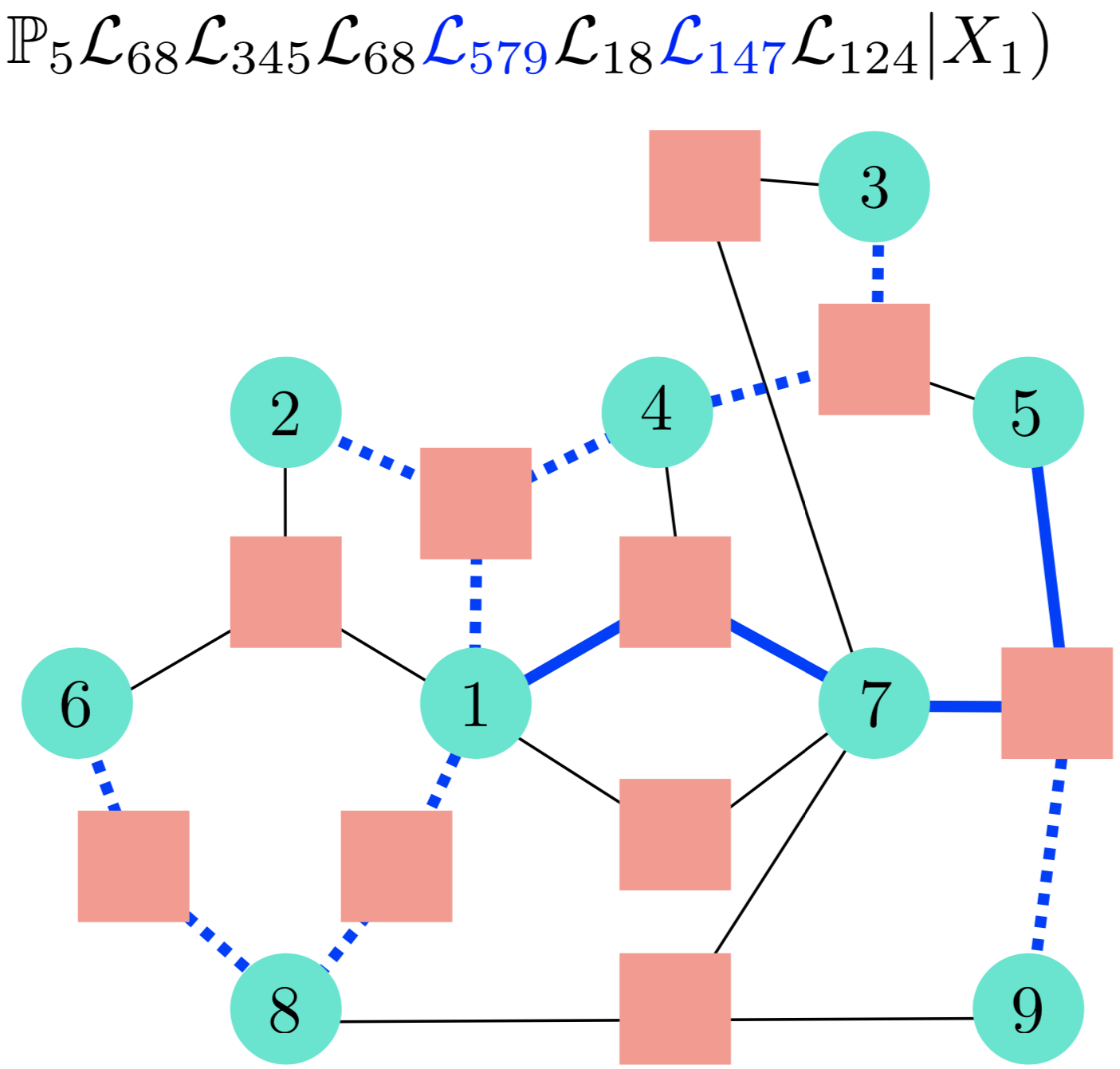
We develop cutting edge methods to constrain the spread of quantum information in many-body devices. We have discovered new mathematics to bound how quickly quantum bits can become correlated and entangled, significantly advancing the state of the art beyond the existing Lieb-Robinson Theorem. Our techniques find broad applications, from the study of quantum gravity and fast scrambling in holographic systems, to the robustness of quantum information processors in noisy experimental devices with long-range interactions, to models of interacting bosons with infinite-dimensional Hilbert spaces.
Quantum Error Correcting Codes
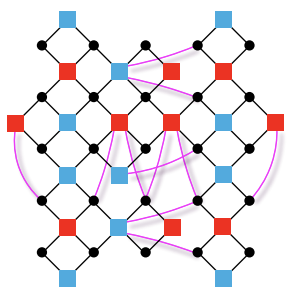
We study quantum error correcting codes, especially from a physics perspective. In particular, we are interested in LDPC (low-density parity-check) codes, which we recently showed are quantum memories with a trivial thermodynamic phase diagram. LDPC codes also gave rise to the first complete mathematical proof of many-body localized eigenstates. More generally, we are also interested in understanding the most general possible open and driven quantum dynamics, which could lead to a systematic classification of quantum dynamical universality classes. We also work with experimental groups to demonstrate new ideas in QEC, including the first demonstration of beyond-break-even state preparation using LDPC codes.
Holographic Quantum Matter
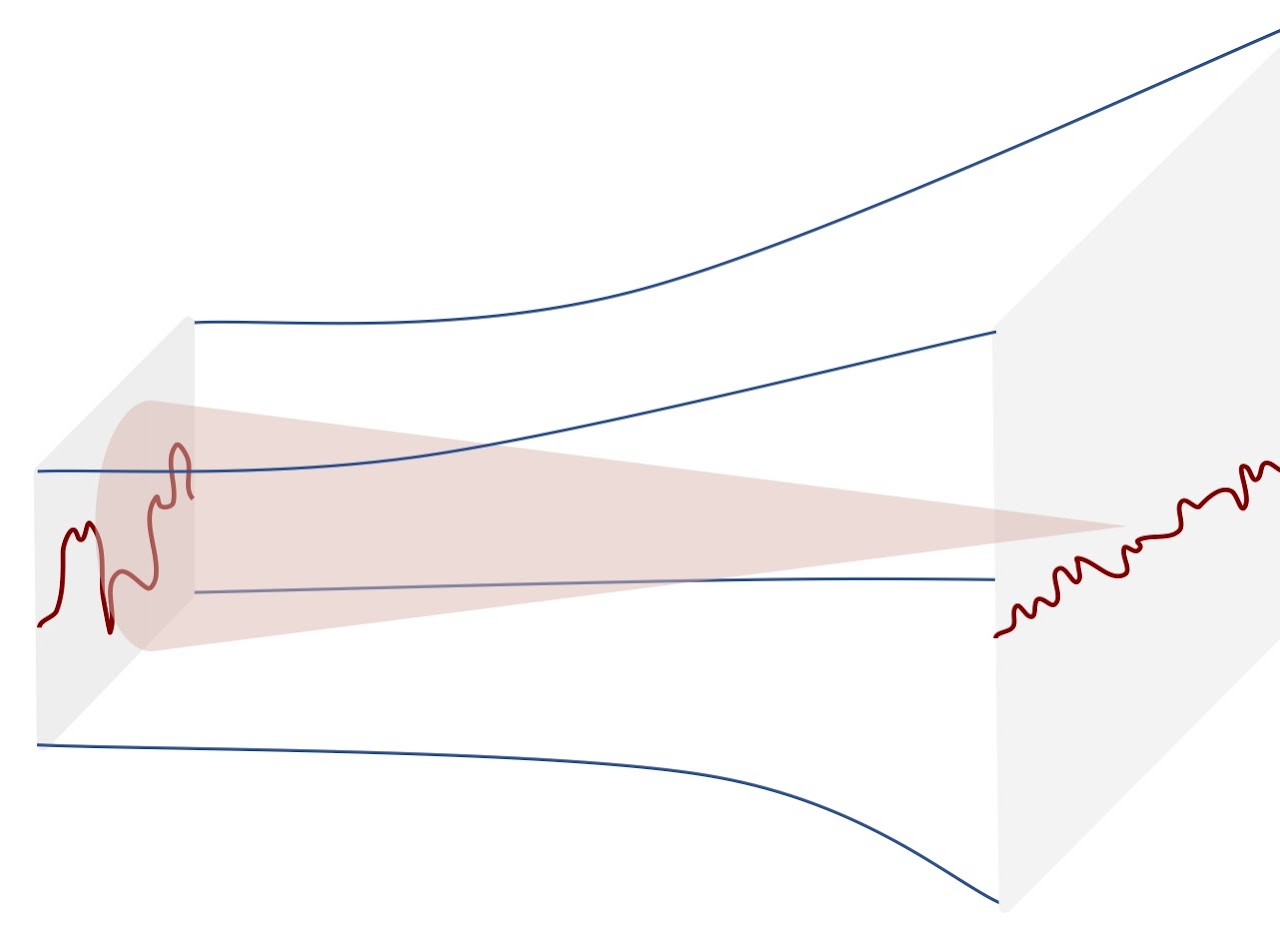
We apply methods from string theory and supergravity to develop cartoon models of strongly coupled quantum matter, a problem relevant for condensed matter physics, nuclear physics and beyond. Our particular focus is on holographic dynamics out of equilibrium, together with the implications and interpretations of these studies using conventional methods, including quantum field theory. Our previous work has included a theory of the transport properties of highly inhomogeneous black holes, where we demonstrated that holographic matter generally avoids disorder-driven metal-insulator transitions.